Methodology Report #7: Construction of Weights for the 1996 MEPS Nursing Home Component
by John Paul Sommers, Ph.D., Agency for Health Care Policy and Research; James Bethel, Ph.D., and Pamela Broene, M.S., Westat, Inc.
Select for more information on
Health Care Information and Electronic Ordering Through the AHRQ Web Site
Abstract
The Medical Expenditure Panel Survey (MEPS) is the third in a series of nationally representative surveys of medical care use and expenditures sponsored by the Agency for Health Care Policy and Research (AHCPR).
MEPS comprises four component surveys. The Nursing Home Component (NHC) produces national estimates of insurance coverage and the use of services, expenditures, and sources of payment for persons residing in or admitted to nursing homes. The NHC also gathers information on nursing home characteristics–such as facility type, ownership, chain affiliation, certification, facility size, and location–for a nationally representative sample of nursing homes. Building on a previous report, this report completes the description of the statistical methodology used in the MEPS NHC. It completes the reporting of response rates and describes the calculation of weights for the remaining sample units necessary to correct for nonresponse.
Select for information on The Medical Expenditure Panel Survey (MEPS).
Purpose
This is the second report from the Agency for Health Care Policy and Research (AHRQ) describing the statistical methodology used in the 1996 Medical Expenditure Panel Survey Nursing Home Component (MEPS NHC). The frame, sample design, allocation and selection processes, and some partial response rates have been presented in a previous publication (Bethel, Broene, and Sommers, 1998). This publication completes the reporting of response rates and describes the calculation of weights for the remaining sample units necessary to correct for nonresponse. Return To Top
Background
The 1996 MEPS NHC was a survey of nursing homes designed to collect information on nursing homes and their residents in the United States during calendar year 1996. The survey consisted of a sample of nursing homes and a sample of residents within the nursing homes. For the purpose of the survey, a nursing home was defined as a facility or distinguishable portion of a larger facility with at least three beds set up for nursing care. To be eligible for the survey, the facility or portion of a facility must have been:
- Certified by Medicare or Medicaid as a nursing facility or
- Licensed by a State as a nursing home with a registered nurse or licensed practical nurse onsite 24 hours a day, 7 days a week.
The sample of facilities was selected from a list frame, the 1994 Health Provider Inventory (HPI). To select the sample, the facilities on the list were stratified into groups defined by facility type, the reimbursement method used in the State, and size. A sample of facilities was selected with probability proportional to the number of facility beds. The sample was then classified into four strata according to the cost of data collection, and each of the four cost strata was subsampled to create an optimal sample given the overall collection budget.
Data collection was accomplished in three rounds during 1996 and early 1997. In each round a sample of residents was selected with equal probability of selection within each facility. During the first round, a sample of persons who were residents in a facility at the beginning of the year was selected. In the remaining two rounds, samples of persons who were admitted during the first and second halves of the year were selected. The average expected sample size for both current residents and new admissions was 4 per facility.
Because persons could reside in more than one facility during a calendar year, special care was taken in the process to select only persons whose stay in a sampled facility was their first stay in any nursing home during the calendar year. This was done to allow accurate calculation of each person’s probability of selection. The calculation was especially problematic for persons who were admitted after the beginning of the year, because they could have had a previous admission to the same or another facility. For this reason, efforts were made to determine whether persons selected as new admissions had had a stay in another facility during the year. Any new admissions selected who were found to have had a previous stay in an eligible facility during the year were dropped from the sample as ineligible. As a result, the approximate number of eligible new admissions in the sample was 3 per facility.
The primary focus of the survey was collection of data on expenditures within the nursing homes during calendar year 1996. Information on other characteristics of the residents also was collected, including demographics, health status, use of other health care, use of prescription medications, and a complete history of the place of residence for each sampled person. Facility characteristics such as size, ownership, charge rates, certification status, and existence of special care units also were collected (Bethel, Broene, and Sommers, 1998; Potter, 1998).
Return To Top
Response Rates
Facilities
The original sample size fielded for the 1996 MEPS NHC was 1,150 facilities. The sample size was based on the assumption that the response rate would be 75 percent and that approximately 5 percent of the sample would be out of scope, providing a final desired sample size of approximately 800 facilities (Bethel, 1995). There were 951 responding facilities with information on 3,791 persons after the end of the first round of data collection, so both the eligibility rate of 98 percent and the response rate of 85 percent were higher than expected. Thus, if a subsample of the original 1,150 facilities was kept for data collection for the last two rounds, money could be saved and the goal of 800 cooperating facilities still could be met.
In order to allow for this possibility, the 1,139 facilities in the sample that had not been selected with certainty (Bethel, Broene, and Sommers, 1998) had been divided into 18 random groups. After the first round of data collection, two of the random groups, 127 facilities, were randomly removed from further data collection. Of these, 108 were respondents, 18 were nonrespondents, and 1 was out of scope. This left 843 responding facilities in the remaining sample, 154 nonrespondents, and 26 out of scope--a total of 1,023 facilities in the smaller, final sample.
After the second round of data collection, 833 facilities had responded. Finally, 815 facilities responded for all three rounds of data collection. Response was defined as allowing sampling of new admissions in each round, as well as providing data for persons sampled within the facility. Therefore, of the 997 in scope facilities in the final sample, 815, or 81.7 percent, were respondents.
Return To Top
Persons
Within each cooperating facility, almost all the persons in the sample were respondents. A sampled person was a respondent if he or she was sampled from a facility that responded for all three rounds of data collection and reported a set of key variables along with a large enough percentage of data from each of six main data groups: health status, expenditures, background, income and assets, health insurance, and prescription medications.
Of the 3,260 current residents selected in the 815 responding facilities, 22 were ineligible, 25 had unknown eligibility, and 4 were nonrespondents. Current residents were ineligible if it was found during data collection that they had not been residents of the sampled facility as of January 1, 1996.
Of the 1,740 new admissions selected in the second round of data collection, 260 were ineligible, 75 had unknown eligibility, and 24 were nonrespondents. Of the 1,726 admissions selected in the third round of data collection, 315 were ineligible, 88 had unknown eligibility, and 14 were nonrespondents. Admissions were declared ineligible if it was found during data collection that they had had a previous stay in a nursing home during the year before the stay for which they were selected. This process, allowing selection for only the first stay within a facility for the year, was used in order to simplify the calculation of the probability of selection for an admission. Losses were anticipated in the sampling process.
Persons with unknown eligibilities were classified as nonrespondents. Thus, of 3,238 current residents considered potentially eligible, 3,209, or 99.1 percent, were respondents conditional on their being sampled within the responding facilities. Of the sample of 2,891 potentially eligible admissions within the responding facilities, 2,690, or 93.0 percent, responded. Multiplying these values by the facility response rate of 81.7 percent resulted in unconditional response rates for the two person-level samples. The unconditional response rate for current respondents was 81.0 percent. The unconditional response rate for admissions was 76.1 percent.
By assuming all persons with unknown eligibility to be nonrespondents and none to be ineligible for response rate calculations, we used the lowest possible value in the numerator and the highest possible value in the denominator for our calculation of person-level response rates. Because it is likely that some of the persons with unknown eligibility would be ineligible (and thus would be removed from the denominator), the rates calculated are conservative lower bounds for the unconditional response rates.
Return To Top
Round 1 Weights
Descriptive facility information was collected in the first round of data collection (Round 1), as was demographic and health status information for the sample of current residents, who were persons in a nursing home as of the beginning of calendar year 1996. This information is ideal for creating a snapshot view of the characteristics of nursing homes and their residents. Because this is valuable information, the data collected in Round 1 were used to make a preliminary set of estimates published by AHCPR and were also released to the public for analyses (Rhoades, Potter, and Krauss, 1998) Those estimates were preliminary, and they differ slightly from the estimates based on data for respondents to all three rounds of data collection given later in this report.
Because the sample units were selected with unequal probabilities and because of nonresponse in the data collection, weights must be calculated for each unit in the original sample, and the weights for respondents--both facilities and persons within the facilities--must be adjusted for nonresponse (Kish, 1965).
To motivate this adjustment, it is assumed that pi is the probability of selection of the ith unit in the sample, and wti = 1/pi, the initial weight. Then
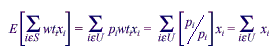
where S and U are the set of sampled units and set of units in the universe, respectively.
A method of making an unbiased estimate of a total from the sample is to use the weighted sum from the sample as the estimate. If there is nonresponse--if, for example, some of the x values are missing--one would try to adjust weights for the values of respondents in cells for which the responding x’s have the same or very similar expected values to those of the nonresponding x’s. Thus, the final objective is to have the sum of weights for respondents over cells with various characteristics equal to the totals from the original sample.
Correction of weights also can be taken further using a technique called poststratification. This method is used when outside information is available about the population. The sum of the weights over a particular characteristic can be thought of as an estimate of the population total for the particular characteristic. Ideally, the total weight for each important subset of the population should equal the population for that subset. Controlling weights so that they equal population totals is called poststratification (Madow, Olkin, and Rubin, 1983; Skinner, Holt, and Smith, 1989).
Given this motivation for weights and adjusting these weights for nonresponse, the description of the methods used to calculate weights for the 951 facilities and 3,791 persons responding in the first round of data collection follows.
Return To Top
Round 1 Facility-Level Weights
In the first step, the probability of selection for each of the 1,150 facilities in the original sample
was calculated (Bethel, Broene, and Sommers, 1998). After the 1,150 initial weights for the original sample were produced, they were adjusted for nonresponse. This was done using a set of 10 cells defined by 4 variables: (1) type of ownership, (2) certification, (3) Beale code, and (4) whether the facility was related to a hospital. These variables, which are correlated with costs as well as characteristics of nursing homes, are defined in the appendix. Because of the number of cells generated by combination of the four variables, cell collapsing was required. Collapsing was based on the sample size in the cell and whether the facilities in the collapsed cells differed in characteristics and/or response rates. Definitions of the collapsed cells used are provided in the appendix.
To adjust for nonresponse within a cell, the standard process was used. The initial weights of all responding units in each cell were increased by multiplying the weight of each respondent in the cell by the ratio of the total of the initial weights for all eligible units in the cell over the sum of the initial weights of all responding units in the cell. Thus, in the case of the Round 1 sample for the MEPS NHC, if the value of ith unit’s initial weight were wti, the adjusted weight for responding units in the response cell C, where CR is the set of respondents in C, would be

Return To Top
The adjusted weights for nonrespondents were set to zero. Weights of ineligible units were left unchanged.
At this point, the list frame of the population was used to provide information. Because the frame is the best description of the population and because this information describes the potential sampling units on the frame, the weights were poststratified so that the sum of the weights for the responding sample and ineligible sample for cells created by four important variables equaled the cell population totals. Ineligible units were included in this process because they represented the number of ineligible units on the frame in the categories used. Therefore, they must be accounted for in any poststratification to the frame, because exact frame totals for eligible units are not available.
The four variables chosen were (1) number of beds in the facility, (2) type of ownership, (3) certification status of the facility, and (4) Beale code (used to indicate the urban or rural location of the facility). These variables, which are correlated with costs as well as characteristics of nursing homes, are defined in the appendix.
Because the number of cells defined by the cross of all levels of these variables was very large, the sum of the weights for each cell created by these cross-classifications was not made equal to the population total. Instead, the weights for each cell defined by any one of the variables alone were made to add to the population total for the particular cell. Thus, for each marginal cell defined by any one of several variables, the totals of the weights were equal to the marginal population totals.
The method can be illustrated with an example. Suppose one were concerned only with two variables: (1) type of ownership, with 3 levels (for profit, not for profit, and governments) and (2) region, with 4 levels (Northeast, South, Midwest, and West). Rather than making the sum of weights in the 12 cells defined by a cross of the two variables (for instance, for profit and South) equal the sum of the number of facilities on the frame, one simply causes the sum of the weights for each of the 7 cells defined by each individual variable (for instance, for profit or South) to equal the number of facilities on the frame. To accomplish this, one uses an iterative technique called raking, which is explained in the following paragraphs (Madow, Olkin, and Rubin, 1983).
Return To Top
Assume that wtijk is the nonresponse-adjusted weight for the ith sample unit in the jkth cell. Also, Nj. is the population total defined by the jth cell of the first variable, and N.k is the population total defined by the kth cell of the second variable. For example, the first variable could break the population by size of nursing home and the second by region of the country. One would adjust the weights to create a set of weights wt9ijk such that:
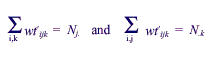
To do this, one first creates values aj such that
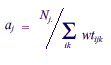
Then,
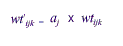
One continues this process through all values of j. This makes sample weight totals sum to the proper values for the first defining variable, but not the second. One then operates on the values of wt9ijk to adjust them so that the sum of the weights for the cells defined by the second variable equals the number of facilities on the frame. Of course, now this third set of weights may not sum properly for cells defined by the first variable. The cycle is repeated, readjusting each new set of weights by continuing to iterate through the process. Usually within several cycles the weights will converge, so that for each cell defined by either of the two variables, the sum of the latest set of weights equals a value very close to the required marginal total. This completes the raking process.
The raking process can be applied to make weights sum to marginal cell totals for as many variables as one likes. In this example, two variables were used to create marginal totals, and the weights were forced to add to the population total for the different sizes of nursing homes and for each region, but not necessarily by size and region. In the adjustment of the MEPS NHC weights to the population sizes determined by the survey frame, the four variables above defined the marginal cells and their totals for the raking process.
As is most often the case, the raking process converged. All the marginal totals produced for eligible and ineligible units were very close to the control totals from the frame used in the process. The maximum relative difference was .00012 of the marginal total. Most differences were on the order of .00001 of the marginal total.
When this adjustment is made, the sum of the facility weights for responding units equals the sum of the number of units on the original frame less the sum of the raked weights of ineligible units. The relationship to the frame is maintained in this method by using the sum of the raked weights of the ineligible units in the sample as an estimate of the ineligible units on the frame. The difference between the total number of units on the frame in a cell and this value would be an estimate of eligible facilities in a cell. After raking, the ineligible units are no longer of use because one is concerned only with eligible nursing homes. Thus, their final raked weight is set to zero.
Return To Top
Round 1 Person-Level Weights
Weights also were calculated for current residents selected in the 951 facilities that responded in the first round of data collection. The following basic weighting techniques were used:
- A base weight is equal to 1 divided by the probability of selection of a unit; the probability of selection would be 1 divided by the weight.
- The sample selection for the MEPS NHC was done in two stages: first, the facilities were selected, and then persons were selected within the selected facilities.
- The weight of a person within a facility is equal to 1 divided by the probability of selection within the facility. For the MEPS NHC, the selection probability is simply the number of current residents on the list for the facility divided by the number of persons selected in the facility. (Note that these numbers include the totals on the list and the totals selected even if some persons in each group were later found to be ineligible, because the ineligibles were used in the selection process.)
Using these concepts, the probability of selection of a person would be the probability of selecting a person within a selected facility multiplied by the probability of selecting the facility. In the case of the first set of responding facilities in the MEPS NHC, an adjusted facility weight had been calculated. This was used as the inverse of the probability of selection of the facility, assuming that subsampling was done to select the respondent nursing home from the original sample. Therefore, the basic weight for a person in the sample before nonresponse at the person level was calculated as the adjusted facility weight multiplied by the number of persons on the selection list within the facility and divided by the number of persons selected from the list within the facility.
After the original probabilities of selection were calculated, adjustments were made for nonresponding persons. A simple two-step adjustment process was chosen because there were so few nonresponding persons. The steps were as follows:
- For any facility with a nonresponding person, if there were 3 sampled persons remaining within the facility (the fixed sample size was 4 unless there were fewer than 4 residents in the facility), the weights for the remaining persons were adjusted by multiplying by 4/3.
- After this adjustment, the persons were broken into two groups: (1) those from hospital-based facilities in States with facility-specific, non-case-mix Medicaid reimbursement methods (those States that do not consider the mix of patients in determining the Medicaid reimbursement that a facility receives) and (2) those from all other facilities. These cells were chosen because the former was the only cell defined by any variables related to nursing home costs or characteristics with any nonresponse after the first correction within facilities. The weights for respondents in the first group were adjusted upward so that their sum equaled the weighted total for the entire group. The second group had no nonrespondents, and no adjustment was made.
Return To Top
Final Weights
Final Facility-Level Weights
After the third round of data collection, facility-level and person-level weights were again calculated. Because the final sample was based on the sample of 1,023 nursing homes in the subsample selected in the first round of data collection, the probability of selection of each of the 1,023 nursing homes was used to produce the basic weights for these facilities. Thus, the process ignored the corrections and weighting done for the first round alone. The process was started again from the beginning sample.
The method used followed the same pattern as for the set of weights produced earlier for data from the first round of data collection. Starting with probabilities of selection, (1) basic weights were produced, (2) weights of respondents were adjusted within cells to account for nonrespondents, and (3) respondent weights were raked to frame totals. The first two steps were performed as before. Basic weights were calculated as the inverse of the probability of selection, and nonresponse adjustments were made using the same set of 10 cells used to produce weights for the first round.
The variables used to provide controls for raking differed somewhat from the calculation of the weights used after the first round of data collection. This change was made because new information existed about variables that were correlated with nonresponse for both facilities and persons. To properly adjust the weights, members of this set of variables needed to be considered if they also were likely to correlate with a respondent’s data.
To accomplish this adjustment, raking to frame values was performed using eight sets of marginal totals defined by the following variables: ownership type, certification status combined with whether a facility was hospital based, Beale code, size class, Census region combined with type of State reimbursement system, cost stratum, whether the survey was endorsed by the State nursing home association, and number of nursing home beds per population age 75 and over in the county. All these variables were available for facilities on the frame except cost stratum, for which estimates from the original sample, before subsampling within each cost stratum, were used as control totals.
As in the previous raking process, this second raking used the set of eligible facility respondents and the ineligible facilities. The nonresponse-adjusted weights were used for responding facilities, and initial weights were used for ineligible units. Again, this was done because the two sets together should produce totals of units equal to the entire frame. These were raked over the eight sets of marginal values. Like the first raking process, this process converged to produce a set of raked facility weights that met the marginal total constraints. The weights for the ineligible units were set to zero, and the weights for responding facilities again represented the eligible units from the frame Return To Top
Final Person-Level Weights
In order to calculate a weight for each person in a facility, a basic weight for each person was calculated in the same fashion used to calculate basic weights for current residents in weighting done for the Round 1 data. A conditional within-facility weight for each selected person was produced, equal to 1 divided by the probability of selecting the person from a facility, given that the facility was selected. This probability was equal to the number of persons selected within the facility divided by the number of persons on the sampling list for the particular round. In the first round, residents were selected as of the beginning of the year. In the later two rounds, persons were selected from a list of admissions. The conditional within-facility weight was then multiplied by the facility weight to obtain the basic person-level weight for each person selected.
At this point the data were ready to be adjusted for person-level nonresponse. Because of obvious differences in length of stay, expenditures, and characteristics, persons selected in each round were adjusted in separate although identical steps. The first step was to adjust for nonresponse due to unknown eligibility in each of the three groups: current residents, second-round admissions, and third-round admissions. The sum of the weights for persons with unknown eligibility in each of the groups of sampled persons was distributed proportionally across the remaining sample in the group for both eligible and ineligible members.
As an example, suppose that, in a particular round of sampled persons, 60 percent of the total weight belonged to eligible persons, 30 percent to ineligible persons, and 10 percent to persons with unknown eligibility. In this case, for those persons with known eligibility, two-thirds (60/(60 + 30)) were eligible, and thus two-thirds of the unknown 10 percent of the weights were assigned to the eligible persons. This gave them 66.7 percent of the total weight, and the other one-third of the 10 percent unknown weight was assigned to those persons known to be ineligible. The weights for persons with unknown eligibility were set to zero. The increase for all persons with known eligibility status was the same. The basic weight for each person with known eligibility remained essentially the same percentage of those with known eligibility as before the adjustment. To make this adjustment, the weight for each person with known eligibility is multiplied by 1 divided by the percentage of the weight represented by persons with known eligibility. In the example, this factor would be 1/.9.
The second step for each of the three groups was to adjust the weights for respondents who were eligible so that they would add to the total weights for all eligible persons in the group, both respondents and nonrespondents. The process used for current residents, those selected in the first round, was the same as that used for the set of weights previously discussed for first-round respondents. Adjustments were made for any person from a facility with only one nonrespondent by adjusting the weights for the remaining persons selected in the facility. After this adjustment, the persons were divided into the two groups described previously (those from hospital-based facilities in States with facility-specific, non-case-mix Medicaid reimbursement methods and those from all other facilities), and the weights for respondents in each group were increased to adjust for the nonrespondents. Because the nonresponse was so small, adjustment factors were not very different from 1.
For the two sets of persons selected as new admissions during Rounds 2 and 3, the adjustment after that for unknown eligibility was different. For these two groups, nonresponse, although represented by a small fraction of the eligible persons, was correlated with the length of a person’s stay in the nursing home, which was obtained during sampling. The eligible persons in each of the two groups were broken into three cells based on length of stay:
0 <= length of stay <= 20 days
21 <= length of stay <= 60 days
61 days <= length of stay
Within each group, the respondents’ weights were adjusted upward to account for the weight of the nonrespondents. Return To Top
Trimmed Weights for New Admissions
After completion of the weighting process described above, the weights were reviewed. During this review, the weights for new admissions were determined to be highly skewed because a number of smaller hospital-based nursing homes had extremely large numbers of admissions relative to the numbers of beds within the facilities. Because the sample size within each facility was limited to control the data collection burden within the facility (Bethel, Broene, and Sommers, 1998), the conditional probability of selection for an admission within each facility was quite small; as a result, the inverse of this value--the within-facility weight--was very large, and the overall person weight was very large. However, less than 1 percent of the persons in the sample of eligible admissions accounted for about 18 percent of the total population of admissions represented in the MEPS NHC, and the variances for the estimates of total admissions were therefore very high. The relative standard error for the estimate of the national total of admissions was more than 8 percent. To lower these variances, the weights for the new admissions in smaller hospital-based nursing homes were trimmed. Trimming is a process that lowers the weights for the persons with excess weights by distributing some of those weights to the remaining sample.
A simple example illustrates the process. Suppose that one has a sample that can be broken into two sets. The sample in the first set contains 80 percent of the total of all weights and the second contains 20 percent. However, suppose that the second set has only a small number of sample units. Suppose further that one decides to restrict the total weight of the second group to 10 percent of the total. To do this, one proportionally redistributes the 10 percent of weights from the second set to the first set of sample units by multiplying the weights for each unit in the first set by the new total they are to represent, divided by the original total weight for the first set. In the example, the factor would be .9/.8.
Upon review of a selected set of estimates made with (1) the original untrimmed weights, (2) a test set of weights created by allocating the trimmed values to all facilities, and (3) the weights created by allocating the trimmed weights only to hospital-based facilities, the estimates made with the last set of weights and those with the first were found to be similar. However, the second set of weights changed some estimates significantly. So, because of the decreased errors, the third set was chosen as the final set of weights for the persons in the sample who were selected as new admissions.
The method was implemented in two steps. First, the 99th percentile of the weights was determined. This value was approximately 6,909. The weight for any unit that had a larger weight (all were hospital-based units) was reduced to this value. The excess was allocated proportionately to the remaining hospital-based units as described in the example. Upon review of this process, it was discovered that the weights for some units that originally were smaller than 6,909 were now larger than 6,909 because of the portion of the excess weight that was allocated to them during the trimming process.
To handle this problem, the set of weights obtained from the first trimming process was trimmed again using the same process. On the second iteration, no weights higher than 6,908 remained. The variances were lowered with these weights. The relative standard error for the national total of admissions was reduced to approximately 6 percent. The revised estimates did not show any significant bias, and the objective of the trimming process was met. Return To Top
Estimates
With the weighting complete, it was possible to produce final estimates for national totals of nursing homes, their current residents on January 1, 1996, and their new admissions during 1996. The estimates are as follows:
- Nursing homes: 16,760.
- Current residents: 1,560,003.
- Persons with admissions who were not residents of a nursing home as of January 1, 1996: 1,536,525.
The relative standard errors of these estimates are 2.5 percent, 1.5 percent, and 6.4 percent, respectively.
Return To Top
References
Bethel JB. Response and eligibility rate assumptions for NNHES. Personal correspondence with John Sommers; 1995.
Bethel J, Broene P, Sommers JP. Sample design of the 1996 Medical Expenditure Panel Survey Nursing Home Component. Rockville (MD): Agency for Health Care Policy and Research; 1998. MEPS Methodology Report No. 4. AHCPR Pub. No. 98-0042.
Kish L. Survey sampling. New York: John Wiley and Sons; 1965.
Madow WG, Olkin I, Rubin DR. Incomplete data in sample surveys, volume 2: theory and bibliographies. New York: Academic Press; 1983.
Potter DEB. Design and methods of the 1996 Medical Expenditure Panel Survey Nursing Home Component. Rockville (MD): Agency for Health Care Policy and Research; 1998. MEPS Methodology Report No. 3. AHCPR Pub. No. 98-0041.
Rhoades J, Potter DEB, Krauss N. Nursing homes––structure and selected characteristics, 1996. Rockville (MD): Agency for Health Care Policy and Research; 1998. MEPS Research Findings No. 4. AHCPR Pub. No. 98-0006.
Skinner CJ, Holt D, Smith TMF. Analysis of complex surveys. New York: John Wiley and Sons; 1989.
Return To Top
Appendix
Definition of Selected Variables
Bed category =
|
| 1 |
if 2 < beds < 88 |
| 2 |
if 87 < beds < 120 |
| 3 |
if 119 < beds < 170 |
| 4 |
if 169 < beds |
Type of ownership=
|
| 1 |
if for profit |
| 2 |
if nonprofit |
| 3 |
if government |
Certification/hospital status =
|
| 1 |
if hospital based |
| 2 |
if certified but not hospital based |
| 3 |
if not certified or hospital based |
| Beale code =
|
| 1 |
if large metro core |
| 2 |
if large metro fringe |
| 3 |
if medium metro |
| 4 |
if lesser metro |
| 5 |
if adjacent to metropolitan statistical
area (MSA) |
| 6 |
if not adjacent to MSA |
Survey endorsed by State association =
|
| 1 |
if yes |
| 2 |
if no |
Region/reimbursement system =
|
| 1 |
if Northeast and prospective system |
| 2 |
if Northeast and case-mix system |
| 3 |
if North Central and prospective system |
| 4 |
if North Central and case-mix system |
| 5 |
if South and prospective system |
| 6 |
if South and case-mix system |
| 7 |
if West and prospective system |
| 8 |
if West and case-mix system |
|
Cost stratum =
|
| 1 |
if full workload in a single geographic area |
| 2 |
if partial workload in single area requiring
considerable travel |
| 3 |
if single facility requiring considerable
travel but within range of other facilities |
| 4 |
if single facility requiring air travel |
Ratio of nursing home beds to
population age 75 and over in county =
|
| 1 |
if first quarter of distribution |
| 2 |
if second quarter of distribution |
| 3 |
if third quarter of distribution |
| 4 |
if fourth quarter of distribution |
Cell definitions used for nonresponse
adjustments for facility weights =
|
| 1 |
if hospital based |
| 2 |
if certified, not hospital based, for profit
in a large metro core |
| 3 |
if certified, not hospital based, for profit
on fringe of a large metro area |
| 4 |
if certified, not hospital based, for profit
in a medium metro area |
| 5 |
if certified, not hospital based, for profit
in a small metro area |
| 6 |
if certified, not hospital based, for profit
adjacent to a metro area |
| 7 |
if certified, not hospital based, for profit
not adjacent to a metro area |
| 8 |
if certified, not hospital based, not for
profit |
| 9 |
if not certified, not hospital based, for
profit |
| 10 |
if not certified, not hospital based, not
for profit |
|
Return To Top
Suggested Citation:
Methodology Report #7: Construction of Weights for the 1996 MEPS Nursing Home Component.
August 1999. Agency for Healthcare Research and Quality, Rockville, MD.
http://www.meps.ahrq.gov/data_files/publications/mr7/mr7.shtml
|
|
